1. Řešte pro $x\in\mathbb R$.

$(a)\ (x+1)(3x^2-3x+2)=0$	$(b)\ x^2+2{,}5x-2{,}24=0$
$(c)\ \dfrac{5x}{x^2-9}=1$	$(d)\ \dfrac{2x}{3x}+\dfrac 2x-4=\dfrac{18}{x^2+3x}$
$(e)\ (x-\sqrt7)^2=1$	$(f)\ x^2-3x+7=3x+17$
$(g)\ x^2-30=2(7-\sqrt5x)$	$(h)\ x^2-5x+2\sqrt3=2(5-x)$
$(i)\ x^4-6x^2+9=3x^3-9x$

2. Obdélník má jednu stranu o 2 cm větší než druhou. Jeho obsah je 24. Určete strany obdélníka.

3. Délka přepony pravoúhlého trojúhelníka je o 2 větší než větší odvěsna. Větší odvěsna je o 7 větší než kratší odvěsna. Urči délky stran trojúhelníka.

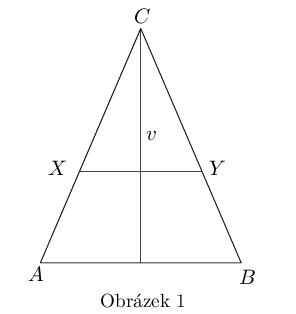
4. Rovnoramenný trojúhelník $\mathsf{ABC}$, který má výšku $v$, je rozdělený úsečkou $\mathsf{XY}$, která je rovnoběžná se základnou $\mathsf{AB}$, tak, že trojúhelník $\mathsf{XYC}$ má stejný obsah jako lichoběžník $\mathsf{ABYX}$. Vypočítejte vzdálenost úsečky $\mathsf{XY}$ od základny $\mathsf{AB}$. (obr. 1)

5. Jak široký musí být žlutý pruh na vlajce (obr. 2) s rozměry $120\times80$ cm², aby zaujímal polovinu plochy vlajky?