D1 | Studijní materiály

1. Upravte výraz $\dfrac {\dfrac {a} {b^{2}}+\dfrac {b} {a^{2}}} {\dfrac {a^{2}-b^{2}} {ab}}:\left( \dfrac {a^{2}-ab+b^{2}} {a-b}\right)$ , $a\ne\pm b$ , $ab\ne0$

$ab$

$\dfrac1{ab}$

$\dfrac1a$

$\dfrac1b$

e) jinak

Řešení	Vybrat Ukázat
$\dfrac{\dfrac{a^3+b^3}{a^2b^2}}{\dfrac{a^2-b^2}{ab}}\cdot\dfrac{a-b}{a^2-ab+b^2}=\dfrac{(a^3+b^3)ab}{(a^2-b^2)a^2b^2}\cdot\dfrac{a-b}{a^2-ab+b^2}=$ $=\dfrac{(a+b)(a^2-ab+b^2)}{ab(a+b)(a^2-ab+b^2)}=\dfrac1{ab}$ Správná odpověď je b).

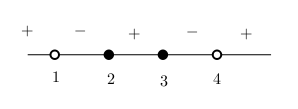
2. Řešením nerovnice $\log_{\frac15}x\le -2$ , $x\in\mathbb R$ je:

$x\in(-\infty;-25)$

$x\in(0;25\rangle$

$x\in\langle25;\infty)$

$x\in(25;\infty)$

e) jinak

Řešení	Vybrat Ukázat
Za podmínky $x>0\quad$ můžeme nerovnici "odlogaritmovat". $\log_{\frac15}x\le -2$ $x\ge\left(\dfrac15\right)^{-2}$ $x\ge25$ Správná odpověď je c).

3. Řešením nerovnice $|x+1|>1$ , $x\in\mathbb R$ je:

$x\in(-\infty;-1)$

$x\in(-\infty;-1\rangle$

$x\in(-2;\infty)$

$x\in\langle-2;\infty)$

e) jinak

Řešení	Vybrat Ukázat
$\|x+1\|>1$ $x+1<-1\qquad\vee\qquad x+1>1$ $x<-2\qquad\vee\qquad x>0$ Správná odpověď je e).

4. Komplexní číslo $=i^{21}$ je rovno:

$z=1$

$z=-1$

$z=i$

$z=-i$

e) jinak

Řešení	Vybrat Ukázat
$i^{21}=i\cdot (i^4)^5=i\cdot 1^5=i$ Správná odpověď je c).

5. Číslo ${3\choose0}+{3\choose1}+{3\choose2}+{3\choose3}$ je rovno číslu:

a) 3

b) 8

c) 6

d) 10

e) jinak

Řešení	Vybrat Ukázat
${3\choose0}+{3\choose1}+{3\choose2}+{3\choose3}=1+3+3+1=8$ Správná odpověď je b).

6. Maximální definiční obor funkce $f(x)=\sqrt{3^x-81}$ tvoří právě všechna $x\in\mathbb R$ , pro která platí:

$x\in(-\infty;4\rangle$

$x\in(-\infty;3\rangle$

$x\in(3;\infty)$

$x\in\langle4;\infty)$

e) jinak

Řešení	Vybrat Ukázat
$3^x-81\ge0$ $3^x\ge81=3^4$ $x\ge4$ Správná odpověď je d).

7. Řešením nerovnice $\dfrac {3x-6} {x+5}\geq 0$ jsou všechna $x\in\mathbb R$ , pro která platí:

a) $x\in(-5;2)$	b) $x\in(-\infty;-5)\cup\langle2;\infty)$	c) $x\in(0;\infty)$
d) $x\in\mathbb R-\{5\}$		e) jinak

Řešení	Vybrat Ukázat
Správná odpověď je b).

8. Nalezněte střed úsečky $\mathsf{AB}$ , kde $\mathsf A=[1;-1]$ , $\mathsf B=[6;-5]$ .

$[-3;\frac72]$

$[2;-3]$

$[\frac72;-3]$

$[-3;2]$

e) jinak

Řešení	Vybrat Ukázat
$\mathsf S_{AB}=\left[\dfrac{x_A+x_B}2;\dfrac{y_A+y_B}2\right]=\left[\dfrac{1+6}2;\dfrac{-1-5}2\right]=\left[\dfrac{7}2;-3\right]$ Správná odpověď je c).

9. Posloupnost je dána svým $n$ -tým členem $a_n=\dfrac {n^{2}-3n+1} {2n^{2}-6n+1}$ , vypočtěte první člen této posloupnosti:

$3$

$-3$

$\dfrac13$

$-\dfrac13$

e) jinak

Řešení	Vybrat Ukázat
$a_1=\dfrac{1^2-3+1}{2\cdot1^2-6+1}=\dfrac{-1}{-3}=\dfrac13$ Správná odpověď je c).

10. Maximálně zjednodušte výraz: $\dfrac {-\sin ^{2}x-\cos ^{2}x} {\sin x}\cdot \left( -\cos x\right)$ , $x\ne k\pi$ , $k\in\mathbb Z$ , $x\in\mathbb R$ .

$\sin x$

$\cos x$

$\text{tg}\,x$

$\text{cotg}\,x$

e) jinak

Řešení	Vybrat Ukázat
$\dfrac {-\sin ^{2}x-\cos ^{2}x} {\sin x}\cdot \left( -\cos x\right)=\dfrac{-(-\cos x)}{\sin x}=\text{cotg}\, x$ Správná odpověď je d).

11. Komplexní číslo $z=\dfrac {2} {1+i}$ převeďte na goniometrický tvar:

a) $z=1-i$	b) $z=\sqrt {2}\left( \cos \dfrac {3\pi } {2}+i\sin \dfrac {3\pi } {2}\right)$	c) $z=\sqrt {2}\left( \cos \dfrac {\pi } {2}+i\sin \dfrac {\pi } {2}\right)$
d) $z=1+i$		e) jinak

Řešení	Vybrat Ukázat
$z=\dfrac {2} {1+i}=\dfrac{2(\cos 0+i\sin0)}{\sqrt2(\cos\frac\pi4+i\sin\frac\pi4)}=\sqrt2[\cos(-\frac\pi4)+i\sin(-\frac\pi4)]=$ $=\sqrt2(\cos\frac{7\pi}4+i\sin\frac{7\pi}4)$ Správná odpověď je e).

12. Mezi čísla $-3$ a $9$ vložte pět čísel tak, aby vznikla aritmetická posloupnost. Součet těchto pěti vložených čísel je:

a) 15

b) 13

c) 11

d) 17

e) jinak

Řešení	Vybrat Ukázat
$\Sigma=S_7-a_1-a_7=\dfrac72(-3+9)-(-3)-9=15$ Správná odpověď je a).

13. Najděte $x\in\mathbb R$ , taková, která splňují nerovnici: $\dfrac {x^{2}-5x+6} {x^{2}-5x+4}\geq 0$

a) $x\in(1;2\rangle\cup\langle3;4)$	b) $x\in\langle1;2\rangle\cup\langle3;4\rangle$	c) $x\in(-\infty;1\rangle\cup\langle2;3\rangle\cup\langle4;\infty)$
d) $x\in(-\infty;1)\cup\langle2;3\rangle\cup(4;\infty)$		e) jinak

Řešení	Vybrat Ukázat
$\dfrac {x^{2}-5x+6} {x^{2}-5x+4}\geq 0$ $\dfrac {(x-3)(x-2)} {(x-1)(x-4)}\geq 0$ Správná odpověď je d).

14. Odchylka vektorů $\vec a$ , $\vec b$ , kde $\vec a=(1;0)$ a $\vec {b}=\left( \dfrac {\sqrt {3}} {2};\dfrac {1} {2}\right)$ je:

$0$

$\dfrac\pi6$

$\dfrac\pi4$

$\dfrac\pi3$

e) jinak

Řešení	Vybrat Ukázat
$\cos\varphi=\dfrac{1\cdot\frac{\sqrt3}2+0\cdot\frac12}{\sqrt{1+0}\cdot\sqrt{\frac34+\frac14}}=\dfrac{\sqrt3}2=\cos\frac\pi6$ Správná odpověď b).

15. Určete množinu všech $x \in \mathbb R$ , pro která platí $|x - 1| + |4 -x| > x + 2$ .

a) $x\in(1;7)$	b) $x\in(-\infty;1\rangle\cup\langle7;\infty)$	c) $x\in(-\infty;0)\cup(7;\infty)$
d) $x\in(-\infty;1)\cup(7;\infty)$		e) jinak

Řešení	Vybrat Ukázat
$a)\quad x\le1$ $1-x+4-x>x+2$ $\underline{\text{x<1}}$ $b) \quad 1<x\le4$ $x-1+4-x>x+2$ $1>x\ \Rightarrow\ \emptyset$ $c) \quad x>4$ $x-1-4+x>x+2$ $\underline{x>7}$ Správná odpověď je d).

Napsat komentář Zrušit odpověď na komentář