A1 | Studijní materiály

1. Podíl $\dfrac{1-\sqrt3}{1+|2-\sqrt3|+2|1-\sqrt3|}$ je roven číslu:

$2-\sqrt3$

$\sqrt3+1$

$\sqrt3-1$

$\sqrt3+2$

e) jinak

Řešení	Vybrat Ukázat
$\dfrac{1-\sqrt3}{1+2-\sqrt3+2\sqrt3-2}=\dfrac{1-\sqrt3}{1+\sqrt3}=\dfrac{(1-\sqrt3)^2}{-2}=\sqrt3-2$ Správná odpověď je e)

2. Součin $\sqrt[6]3\cdot\sqrt[3]{3^2}\cdot\sqrt3$ je roven číslu:

$\sqrt[6]{3^5}$

$\sqrt[18]{3^4}$

$3\sqrt[3]3$

$9$

e) jinak

Řešení	Vybrat Ukázat
$3^{\frac16}\cdot3^{\frac23}\cdot3^{\frac12}=3^{\frac{1+4+3}6}=3^{\frac43}=3\cdot\sqrt[3]3$ Správná odpověď je c).

3. Rovnice $x^2 + 2x + m^2 = 0$ s neznámou $x\in\mathbb R$ a reálným parametrem $m$ má dva různé reálné kořeny právě pro všechna $m \in\mathbb R$ , pro která platí:

a) $m\in(-2;2)$	b) $m\in(-\infty;2)\cup(2;\infty)$	c) $m\in(-1;1)$
d) $m\in(-1;0)\cup(0;1)$		e) jinak

Řešení	Vybrat Ukázat
Diskriminant rovnice musí být kladný. $D=4-4m^2>0$ $m^2-1<0$ $(m+1)(m-1)<0$ $m\in(-1;1)$ Správná odpověď je c).

4. Nerovnice $\left(\dfrac12\right)^x < 1$ platí právě pro všechna $x\in\mathbb R$ , pro která:

$x\in(-\infty;0)$

$x\in(0;\infty)$

$x\in\mathbb R$

$x\in\mathbb R-\{0\}$

e) jinak

Řešení	Vybrat Ukázat
$\left(\dfrac12\right)^x < 1\ \Rightarrow\ \left(\dfrac12\right)^x <\left(\dfrac12\right)^0$ $x>0$ Správná odpověď b).

5. Výraz $\log_2 \left(\sqrt{2\cdot\sqrt[3]2}\cdot\sqrt[3]{2\cdot\sqrt2}\right)$ je roven číslu:

$\dfrac23$

$\dfrac32$

$\dfrac56$

$1$

e) jinak

Řešení	Vybrat Ukázat
$\log_2 \left(\sqrt{2\cdot\sqrt[3]2}\cdot\sqrt[3]{2\cdot\sqrt2}\right)=\log_2\left(2^{\frac12}\cdot2^{\frac16}\cdot2^{\frac13}\cdot2^{\frac16}\right)=\log_22^{\frac12+\frac16+\frac13+\frac16}=\log_22^{\frac76}=\dfrac76$ Správná odpověď e).

6. Číslo $\displaystyle{10\choose8}+ {10\choose 9}$ je rovno číslu:

${11\choose2}$

b) 110

${10\choose9}$

${11\choose8}$

e) jinak

Řešení	Vybrat Ukázat
Podle vztahu $\displaystyle{n\choose k}+ {n\choose k+1}={n+1\choose k+1}$ je $\displaystyle{10\choose8}+ {10\choose 9}={11\choose9}$ . Podle vztahu $\displaystyle{n\choose k}={n\choose n-k}$ je $\displaystyle{11\choose9}={11\choose 11-9}={11\choose2}$ Správná odpověď je a).

7. Počet všech reálných řešení rovnice $\sin 2x = \dfrac12$ je na intervalu $\langle0; 2\pi\rangle$ roven číslu:

a) 2

b) 3

c) 4

d) nekonečně mnoho

e) jinak

Řešení	Vybrat Ukázat
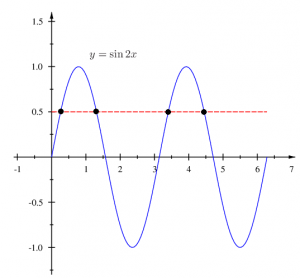
Z grafu funkce $y=\sin2x$ je vidět, že kořeny jsou 4. Správná odpověď je c).

8. Určete, který z následujících bodů leží na přímce procházející body $\mathsf A = [3; -1]$ , $\mathsf B = [2;5]$ :

$[1;10]$

$[0;16]$

$[5;12]$

$[6;-19]$

e) jinak

Řešení	Vybrat Ukázat
Rovnice přímky $\mathsf{AB}$ je $\dfrac{x-3}{y+1}=\dfrac{2-3}{5+1}\ \Rightarrow\ y=17-6x$ . Dosazením souřadnic do rovnice zjistíme, že správná odpověď je d).

9. Množina bodů v rovině popsaná rovnici $x^2 - y^2 - 4x - 6y - 14 = 0$ je:

a) kružnice

b) parabola

c) hyperbola

d) elipsa

e) jinak

Řešení	Vybrat Ukázat
Rovnici upravíme doplněním na čtverec. $x^2 - 4x +4 -(y^2 + 6y+9) =14+4-9$ $(x-2)^2-(y+3)^2=9$ $\dfrac{x-2)^2}9-\dfrac{(y+3)^2}9=1$ Jedná se o rovnici hyperboly. Správná odpověď je c).

10. Imaginární část komplexního čísla $z =\dfrac{1+i}{1-i}$ je rovna číslu:

$1$

$-1$

$i$

$-i$

e) jinak

Řešení	Vybrat Ukázat
Výraz upravíme $\dfrac{1+i}{1-i}\cdot\dfrac{1+i}{1+i}=\dfrac{1+2i-1}2=i$ Správná odpověď je a).

11. Počet všech reálných řešení rovnice $\sin^2x-\sin x = 0$ je na intervalu $\langle0; 2\pi)$ roven číslu:

a) 1

b) 2

c) 3

d) 4

e) jinak

Řešení	Vybrat Ukázat
$\sin^2x-\sin x=0$ $\sin x(\sin x-1)=0$ $\sin x =0 \ \vee\ \sin x=1$ $x_1=0,\qquad x_2=\pi,\qquad x_3=\dfrac\pi2$ Správná odpověď je c).

12. Řešením nerovnice $0 < \log_5 x^2 < 1$ jsou právě všechna $x\in \mathbb R$ , pro která platí:

a) $x\in(-\sqrt5;0)\cup(0;\sqrt5)$	b) $x\in(-\sqrt5;-1)\cup(1;\sqrt5)$
c) $x\in(-\sqrt5;-1)\cup(-1;0)\cup(0;1)\cup(1;\sqrt5)$
d) $x\in\left(-\sqrt5;-\dfrac1{\sqrt5}\right)\cup\left(\dfrac1{\sqrt5};\sqrt5\right)$	e) jinak

Řešení	Vybrat Ukázat
$0<\log_5x^2<1$ $\log_51<\log_5x^2<\log_55$ $1<x^2<5$ a) $1<x^2\ \Rightarrow\ x^2-1>0\ \Rightarrow\ (x-1)(x+1)>0\ \Rightarrow\ x\in I_1=(-\infty;-1)\cup(1;\infty)$ b) $x^2<5\ \Rightarrow\ x^2-5<0\ \Rightarrow\ (x-\sqrt5)(x+\sqrt5)<0\ \Rightarrow\ x\in I_2=(-\sqrt5;\sqrt5)$ $x\in I_1\cap I_2=(-\sqrt5;-1)\cup(1;\sqrt5)$ Správná odpověď je b).

13. Řešením nerovnice $0 < |x + 2| < 1$ jsou právě všechna $x\in\mathbb R$ pro která platí:

a) $x\in(1;3)$	b) $x\in(1;2)\cup(2;3)$	c) $x\in(-3;-1)$
d) $x\in(-3;-2)\cup(-2;-1)$		e) jinak

Řešení	Vybrat Ukázat
$0<\|x+2\|\ \Rightarrow\ x\ne-2$ $\|x+2\|<1\ \Rightarrow\ -1<x+2<1\ \Rightarrow\ -3<x<-1$ $x\in(-3;-2)\cup(-2;-1)$ Správná odpověď je d)

14. Maximální deﬁníční obor funkce $f(x) = \sqrt{x^2 -1} - \log x^2$ tvoří právě všechna $x\in\mathbb R$ , pro která platí:

a) $x\in(1;\infty)$	b) $x\in(0;1)$	c) $x\in(0;\infty)$
d) $x(-\infty;0)\cup(0;\infty)$		e) jinak

Řešení	Vybrat Ukázat
$\begin{cases}x^2-1\ge0\\x^2>0\end{cases}\ \Rightarrow\ \begin{cases}x\in(-\infty;-1\rangle\cup\langle1;\infty)\\x\in(-\infty;0)\cup(0;\infty)\end{cases}\ \Rightarrow\ D_f=(-\infty;-1\rangle\cup\langle1;\infty)$ Správná odpověď je e)

15. Všechny kořeny rovnice $16^x = 3 \cdot 4^x - 2$ leží v intervalu:

a) $x\in(-1;2)$	b) $x\in(2;5)$	c) $x\in(-\infty;0)\cup(3;7)$
d) $x\in(-\infty;-1)$		e) jinak

Řešení	Vybrat Ukázat
$16^x=3\cdot4^x-2$ $(4^x)^2-3\cdot4^x+2=0$ $(4^x-2)(4^x-1)=0$ $x=\frac12\quad \vee\quad x=0$ Správná odpověď je a)

Napsat komentář Zrušit odpověď na komentář