Archiv autora: Rubes
Racionální nerovnice 2
Racionální nerovnice 1
Rovnice s absolutní hodnotou
Kvadratické nerovnice
Kvadratické rovnice 6
1. Řešte pro  .
.
 |
 |
 |
 |
 |
 |
 |
 |
| Řešení | Ukázat |
|---|---|
2. Řešte pro  .
.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Řešení | Ukázat |
|---|---|
3. Čísla  a
a  jsou kořeny rovnice
jsou kořeny rovnice  . Vypočítejte
. Vypočítejte  .
.
4. Číslo  je řešením rovnice
je řešením rovnice  . Vypočítejte
. Vypočítejte  .
.
5. Vypočítejte  , jestliže
, jestliže  .
.
6. Délka jedné odvěsny pravoúhlého trojúhelníka je 75 % délky druhé odvěsny. Obsah trojúhelníka je 48 cm2. Jaký je jeho obvod?
Kvadratické rovnice 5
1. Řešte pro  .
.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Řešení | Ukázat |
|---|---|
2. Koupil jsem květiny za 540 Kč. Kdyby každá květina byla o 1 Kč levnější, mohl bych koupit za stejnou částku o 27 květin víc. Kolik stojí květiny?
3. Brigádník vydělal druhý týden o tolik procent více než první týden, kolik stovek korun vydělal první týden. Kolik vydělal první týden, když druhý týden vydělal 864 Kč?
4. V cisterně je 20 hl čistého alkoholu. Část alkoholu odlijeme a doplníme cisternu vodou. Znovu odlijeme stejný objem směsi a doplníme vodou. Nyní je v cisterně 25% roztok alkoholu. Kolik vody jsme doplnily do cisterny poprvé?
5. Manželce stačí na dovolené určitá částka peněz na dobu o 9 dní kratší než jejímu manželovi. Když jsou na dovolené spolu, stačí jim tato částka na 20 dní. Kolik dní mùže být na dovolené sám manžel?
6. Dva dělníci udělají určitou práci za 12 hodin. Mladší z nich by práci udělal sám za dobu o 10 hodin kratší než starší. Jak dlouho by trvala práce mladšímu dělníkovi?
Kvadratické rovnice 4
Kvadratické rovnice 3
1. Řešte pro  .
.
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Řešení | Ukázat |
|---|---|
2. Obdélník má jednu stranu o 2 cm větší než druhou. Jeho obsah je 24. Určete strany obdélníka.
3. Délka přepony pravoúhlého trojúhelníka je o 2 větší než větší odvěsna. Větší odvěsna je o 7 větší než kratší odvěsna. Urči délky stran trojúhelníka.
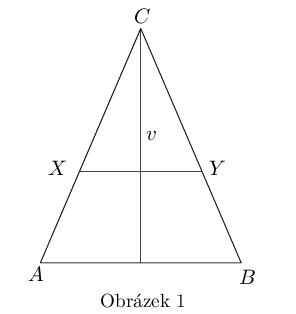
4. Rovnoramenný trojúhelník  , který má výšku
, který má výšku  , je rozdělený úsečkou
, je rozdělený úsečkou  , která je rovnoběžná se základnou
, která je rovnoběžná se základnou  , tak, že trojúhelník
, tak, že trojúhelník  má stejný obsah jako lichoběžník
má stejný obsah jako lichoběžník  . Vypočítejte vzdálenost úsečky
. Vypočítejte vzdálenost úsečky  od základny
od základny  . (obr. 1)
. (obr. 1)
 |
 |
5. Jak široký musí být žlutý pruh na vlajce (obr. 2) s rozměry  cm2, aby zaujímal polovinu plochy vlajky?
cm2, aby zaujímal polovinu plochy vlajky?































































































































































































































































































































































































![\displaystyle \left[1-a^2(1+a^2)^{-1} \right]^{-1}=](http://materialy.rubesz.cz/wp-content/plugins/latex/cache/tex_fa09f4b2fc453a9ae5ab9d0e5213fc1d.gif)
![\displaystyle \left[1-(1-3x)^{-1}\right]\cdot\left[1-(3x+1)^{-1} \right]=](http://materialy.rubesz.cz/wp-content/plugins/latex/cache/tex_e1602c223fe06242b5a9c5c50c5666dd.gif)
![\displaystyle \left[a(a-2)^{-1}-a(a+2)^{-1}\right]:\frac{4}{a^3-2a^2}=](http://materialy.rubesz.cz/wp-content/plugins/latex/cache/tex_e59b80d55fc6082490c0be17bccc9fda.gif)
![\displaystyle \left[(c^2-1)^{-1}+1\right]^{-2}:(1-c^{-4})=](http://materialy.rubesz.cz/wp-content/plugins/latex/cache/tex_ce604f4b17ca9c8a0e75e0f641634a09.gif)
![\displaystyle \left[\frac{x^2-9}{x+1}:\frac{x-3}{1-x^2} \right]^{-1}=](http://materialy.rubesz.cz/wp-content/plugins/latex/cache/tex_9d7ed10f77be70a3e22ceaca777126fb.gif)




![\displaystyle \left[(1-v)^{-1}+(1+v)^{-1}\right]^{-1}=](http://materialy.rubesz.cz/wp-content/plugins/latex/cache/tex_9da91b4bee3a6bac47978a27bba0a7a4.gif)



![\displaystyle \left[\left(\frac{a+1}{2}\right)^{\frac{1}{2}}+\left(\frac{a-1}{2}\right)^{\frac{1}{2}} \right]^2=](http://materialy.rubesz.cz/wp-content/plugins/latex/cache/tex_271f29f3404a7c670d6cf0459d0dd09f.gif)